좋은 알고리즘이란? / 하나의 문제, 여러 가지 알고리즘
하나의 문제에는 여러가지 해결 방법(알고리즘)이 존재한다.
Ex) 알파벳 순으로 되있는 도서관에서 책 찾는 방법
탐색
- 선형 탐색 알고리즘 (linear search algorithm)
- 이진 탐색 알고리즘 (binary search algorithm)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53] 이라는 배열이 존재할 때 29 값 찾는 방법
선형 탐색 : 처음 값 '2' 부터 '3', '5'... 순서로 값을 확인
이진 탐색 : 중간 값 '19' 와 찾는 값 '29' 의 대소를 비교하면 중간 값이 더 작으므로 중간 값보다 작은 왼쪽 원소들은 모두 제외한 후 [23, 29, 31, 37, 41, 43, 47, 53] 배열만 본다. 남은 배열에서 중간값 '37' 과 찾는 값 '29' 의 대소를 비교하면 중간 값이 더 크므로 중간 값보다 큰 오른쪽 원소들은 모두 제외한 후 [23, 29, 31] 배열만 본다. 남은 배열에서 중간값 '29' 와 찾는 값 '29' 를 비교한다. 이렇게 답을 확인한다. (이진 탐색은 선형 탐색과 달리, 정렬된 리스트를 전제로 한다.)
탐색 알고리즘 비교
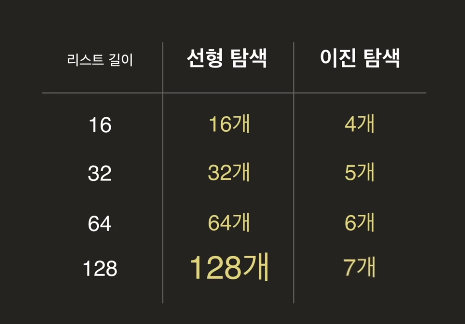
탐색할 값이 많아질수록 선형 탐색과 이진 탐색의 경우의 수는 더 크게 차이난다.
하지만 선형 탐색이 안좋은 것만은 아니다. 이진 탐색은 정렬된 배열만 탐색 가능하다는 등 상황에 따라 다른 탐색을 사용할 수 있다.
(정렬이 안된 배열은 보편적으로 정렬 후 이진 탐색이 가장 빠르다고 한다.)
정렬
리스트의 원소들을 특정 순서로 정리하는 것
- 선택 정렬 (Selection Sort)
- 삽입 정렬 (Insertion Sort)
[4, 2, 7, 1, 9, 3] 배열을 작은 순서대로 정렬하는 방법
선택 정렬 : 인덱스 0부터 차례대로 값을 확인하여 최솟값을 확인한다. 인덱스 3의 값 1이 가장 작기 때문에 인덱스 0과 인덱스 3의 값을 교체한다. 인덱스 1부터 차례대로 값을 확인하여 최솟값을 확인한다. 인덱스 1의 값 2가 가장 작기 때문에 그대로 둔다. 인덱스 2부터 차례대로 값을 확인하여 최솟값을 확인한다. 인덱스 5의 값 3이 가장 작기 때문에 인덱스 2와 5의 값을 교체한다. (생략) 반복하면 [1, 2, 3, 4, 7, 9] 로 정렬된다.
[4, 2, 7, 1, 9, 3] -> [1, 2, 7, 4, 9, 3] -> [1, 2, 7, 4, 9, 3] -> [1, 2, 3, 4, 9, 7] -> [1, 2, 3, 4, 7, 9]
삽입 정렬 : 일단 인덱스 0부터 1까지만 보고 인덱스 0의 값(4)이 인덱스 1의 값(2)보다 크므로 자리를 바꾼다. 이제 인덱스 2까지만 보는데, 이때 인덱스 1의 값(4)보다 인덱스 2의 값(7)이 크므로 그대로 둔다. 그다음, 인덱스 3까지만 보면 인덱스 3의 값(1)이 인덱스 2의 값(7)보다 작으므로 자리를 바꾼다. 바꾼 인덱스 2의 값(1)이 인덱스 1의 값(4)보다 작으므로 자리를 바꾼다. 바꾼 인덱스 1의 값(1)이 인덱스 0의 값(2)보다 작으므로 자리를 바꾼다. 이제 인덱스 4까지 보는데 인덱스 3의 값(7)보다 인덱스 4의 값(9)가 크기 때문에 그대로 둔다. (생략) 반복하면 [1, 2, 3, 4, 7, 9] 로 정렬된다.
[4, 2, 7, 1, 9, 3] -> [2, 4, 7, 1, 9, 3] -> [2, 4, 7, 1, 9, 3] -> [2, 4, 1, 7, 9, 3] -> [2, 1, 4, 7, 9, 3] -> [1, 2, 4, 7, 9, 3] ->
[1, 2, 4, 7, 3, 9] -> [1, 2, 4, 3, 7, 9] -> [1, 2, 3, 4, 7, 9]
정렬 알고리즘 비교
선택 정렬과 삽입 정렬을 살펴보았다. 이 외에도 퀵 정렬, 힙 정렬, 거품 정렬 등 여러 정렬 알고리즘이 있는데, 이 많은 정렬 알고리즘 중 어떤 게 가장 좋을까?
https://www.toptal.com/developers/sorting-algorithms
Sorting Algorithms Animations
Animation, code, analysis, and discussion of 8 sorting algorithms on 4 initial conditions.
www.toptal.com
위 사이트를 들어가면 여러 정렬 알고리즘의 퍼포먼스를 다양한 상황에서 살펴볼 수 있다.
예를 들어 이미 거의 정렬된 리스트를 정렬할 때는 삽입 정렬이 가장 빠른 반면, 무작위 순서의 리스트를 정렬할때는 힙 정렬이 가장 먼저 끝난다. 아예 정반대로 정렬된 리스트의 경우에는 삽입 정렬이 매우 오래 걸린다는 것도 볼 수 있다. 선택 정렬과 합병 정렬은 상황에 영향을 받지 않고 일정한 시간이 소요된다는 점도 주목할만 하다.
보다시피 정렬 문제의 경우 "절대적인 좋은 답"이란 없다. 상황에 따른 각 알고리즘의 장단점을 파악해야 올바른 알고리즘을 선택할 수 있다. 그렇기 때문에 문제를 해결하는 방법을 넘어서 알고리즘을 평가하는 능력을 길러야 한다. (때문에 다음 챕터에서 배울 내용이 바로 "알고리즘 평가법" 이다.)
'Codeit > 알고리즘의 정석' 카테고리의 다른 글
| 알고리즘 패러다임 / Divide and Conquer [1/2] (9) | 2021.04.01 |
|---|---|
| 알고리즘 패러다임 / Brute Force (0) | 2021.03.31 |
| 재귀 함수 / 재귀 함수 (0) | 2021.03.30 |
| 좋은 알고리즘이란? / 알고리즘 평가법 (0) | 2021.03.29 |
| 좋은 알고리즘이란? / 알고리즘이란? (0) | 2021.03.27 |





댓글