728x90
알고리즘 패러다임 / Brute Force
알고리즘 패러다임 : 자주 나타나는 알고리즘 접근법
Brute Force : 가장 순진한 알고리즘 접근법 (모든 경우의 수의 값을 다 구해서 정답을 도출)
Brute Force 의 장점 : 직관적이고 명확하다. 답을 확실하게 찾을 수 있다.
인풋이 엄청 큰 경우에는 Brute Force 알고리즘을 쓰면 오래걸리겠지만, 효율적인 알고리즘의 항상 첫 시작은 Brute Force 이다. Brute Force 방법으로 알고리즘을 한번 생각해보고 거기서부터 발전을 시키는 것이다. 이것이 Brute Force 이해의 필요성이다.
def max_product(left_cards, right_cards):
new_cards = []
for i in left_cards:
for j in right_cards:
new_cards.append(i * j)
return max(new_cards)
#테스트
print(max_product([1, 6, 5], [4, 2, 3]))
print(max_product([1, -9, 3, 4], [2, 8, 3, 1]))
print(max_product([-1, -7, 3], [-4, 3, 6]))
#<Run>
#24
#32
#28Brute Force 알고리즘 - 카드 최대 곱 찾기
왼쪽 카드 뭉치에서 한 장, 오른쪽 카드 뭉치에서 한 장을 뽑아서 두 카드에 적힌 수의 곱이 최대가 되는 값을 리턴
# 제곱근 사용을 위한 sqrt 함수 불러오기
from math import sqrt
# 두 매장의 직선 거리를 계산해 주는 함수
def distance(store1, store2):
return sqrt((store1[0] - store2[0]) ** 2 + (store1[1] - store2[1]) ** 2)
# 가장 가까운 두 매장을 찾아주는 함수
def closest_pair(coordinates):
# 현재까지 본 가장 가까운 두 매장
pair = [coordinates[0], coordinates[1]]
for i in range(len(coordinates) - 1):
for j in range(i + 1, len(coordinates)):
store1, store2 = coordinates[i], coordinates[j]
# 더 가까운 두 매장을 찾으면 pair 업데이트
if distance(pair[0], pair[1]) > distance(store1, store2):
pair = [store1, store2]
return pair
# 테스트
test_coordinates = [(2, 3), (12, 30), (40, 50), (5, 1), (12, 10), (3, 4)]
print(closest_pair(test_coordinates))
#<Run>
#[(2, 3), (3, 4)]Brute Force 알고리즘 - 가까운 매장 찾기
직선 거리가 가장 가까운 매장 찾기 (직선 거리는 distance 함수 이용하기)
시간 복잡도 : O(n^2)
def trapping_rain(buildings):
# 총 담기는 빗물의 양을 변수에 저장
total_height = 0
# 리스트의 각 인덱스을 돌면서 해당 칸에 담기는 빗물의 양을 구한다
# 0번 인덱스와 마지막 인덱스는 볼 필요 없다
for i in range(1, len(buildings) - 1):
# 현재 인덱스를 기준으로 양쪽에 가장 높은 건물의 위치를 구한다
max_left = max(buildings[:i])
max_right = max(buildings[i:])
# 현재 인덱스에 빗물이 담길 수 있는 높이
upper_bound = min(max_left, max_right)
# 현재 인덱스에 담기는 빗물의 양을 계산
# 만약 upper_bound가 현재 인덱스 건물보다 높지 않다면, 현재 인덱스에 담기는 빗물은 0
total_height += max(0, upper_bound - buildings[i])
return total_height
# 테스트
print(trapping_rain([0, 3, 0, 0, 2, 0, 4]))
print(trapping_rain([0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]))Brute Force 알고리즘 - 강남역 폭우
건물과 건물 사이의 빗물의 양을 리턴해주기 (사진 참고)
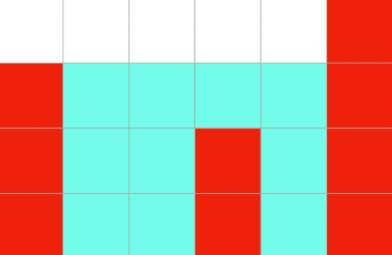
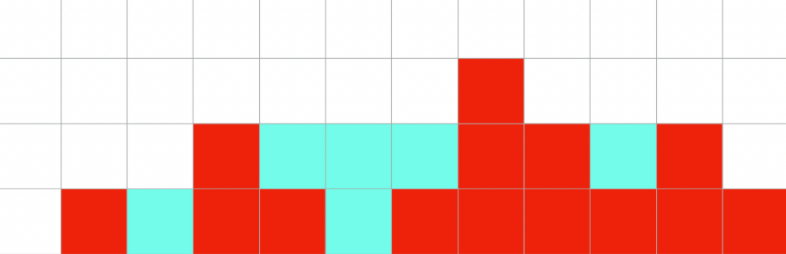
문제 해결 알고리즘 : 우선, 0번 인덱스와 마지막 인덱스에는 빗물이 담길 수 없다. 그리고 현재 인덱스의 왼쪽에서 가장 높은 건물의 높이와 현재 인덱스의 오른쪽에서 가장 높은 건물의 높이 중에서 더 낮은 건물의 높이에서 현재 인덱스에 있는 건물의 높이를 빼면 해당 인덱스에 담기는 빗물의 양이 나온다.
'Codeit > 알고리즘의 정석' 카테고리의 다른 글
| 알고리즘 패러다임 / Divide and Conquer [1/2] (9) | 2021.04.01 |
|---|---|
| 재귀 함수 / 재귀 함수 (0) | 2021.03.30 |
| 좋은 알고리즘이란? / 알고리즘 평가법 (0) | 2021.03.29 |
| 좋은 알고리즘이란? / 하나의 문제, 여러 가지 알고리즘 (0) | 2021.03.28 |
| 좋은 알고리즘이란? / 알고리즘이란? (0) | 2021.03.27 |





댓글